チェバの定理・メネラウスの定理とは?図形問題に強くなる使い分けと覚え方を完全解説!
チェバの定理・メネラウスの定理の意味・違い・覚え方をイラスト付きで徹底解説!高校数学・共通テスト・数学検定でよく出る図形問題対策に。語呂合わせ・使い分け・応用例も網羅!
チェバの定理・メネラウスの定理って何?どこで使うの?
「三角形の図形問題が出ると、どっちの定理を使えばいいか分からない…」
そんな悩みを抱える高校生は多いはず。実は、「チェバの定理」と「メネラウスの定理」は、三角形の内部か外部か、点の位置関係で使い分けが必要です。
これらは図形の“比”を扱う非常に強力な武器。この記事では、定理の意味・使い方・覚え方・違いまで、網羅的に分かりやすく解説していきます。
チェバの定理とは?
チェバの定理は、三角形の内部にある1点から各辺に線を引いたときに使える定理です。
メネラウスの定理とは?
メネラウスの定理は、三角形の各辺またはその延長上にある3点が一直線上にある場合に使える定理です。
「共点」ではなく「一直線上」。この使い分けが肝です。
三角形における「共点」と「一直線上」の違い
ここが混乱ポイント!
• チェバの定理:3本の線が1点で交わる(交点)
• メネラウスの定理:3点が一直線上に並ぶ(共線)
図にすると一目瞭然。「内か外か」で判断しましょう。
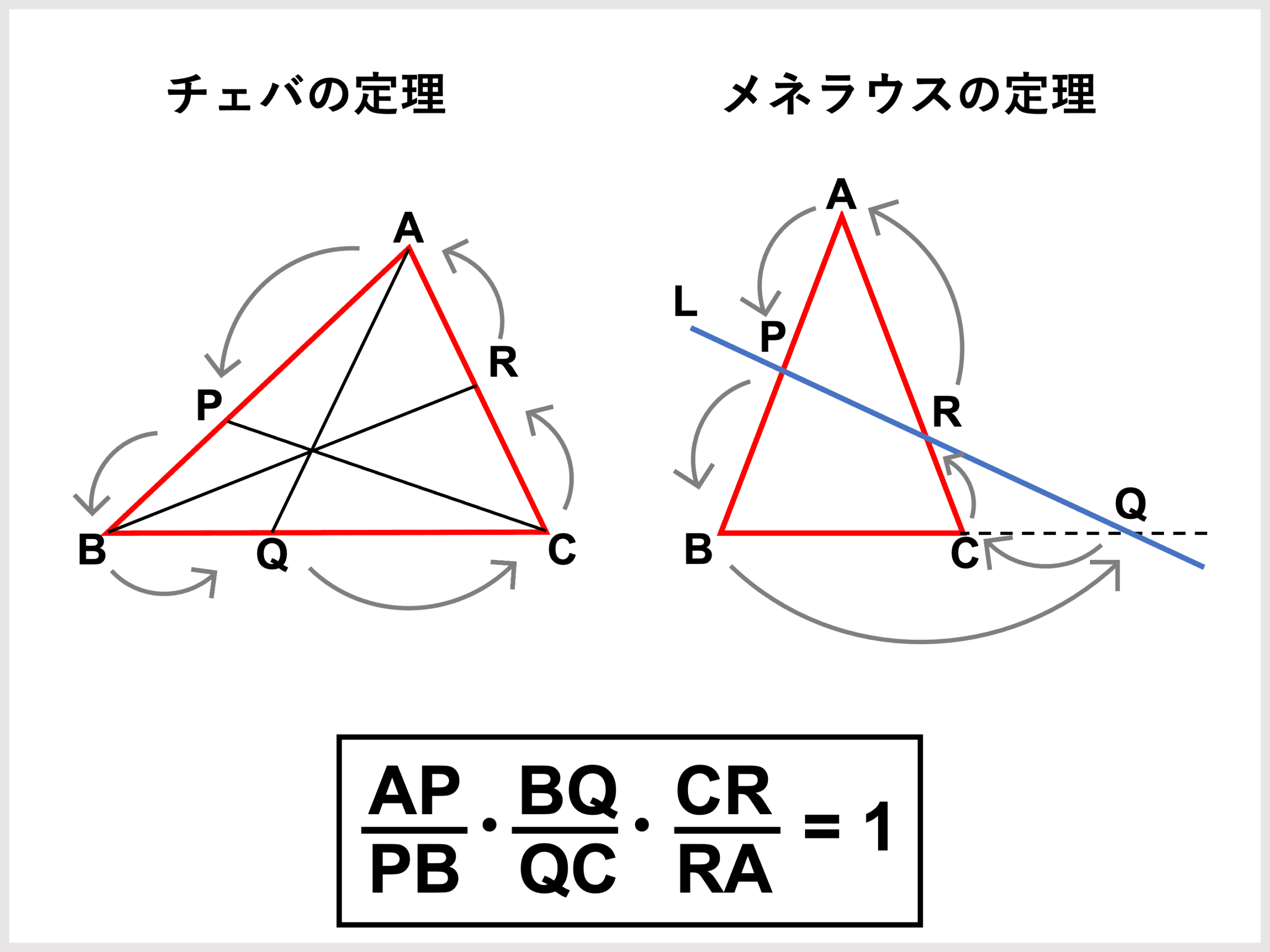
図でわかる定理の構造
📐 チェバ:三角形の内部に点Pがあり、頂点から辺へ線を引くイメージ。
📏 メネラウス:三角形の辺を延長し、外部に点が並ぶイメージ。
どちらも「比の積が1になる」ことが共通しています。
⸻
チェバの定理の式の導出
三角形の相似や面積比を用いて導出できます。
三角形の内部の面積比(AF/FB など)に着目すると理解しやすいです。
⸻
メネラウスの定理の式の導出
一方こちらは、「辺の比(外分・内分)」に注目。
辺をまたいで分数を積み上げるイメージです。注意点は「順番」!
⸻
面積比との関係
例えば「ある点を通る線分が面積を2:1に分けた」などの条件がある場合、
チェバの定理を活用して長さの比を計算できます。これは入試頻出のパターン。
⸻
座標問題での活用例
座標が与えられた場合、比の関係を使って「ある点の座標」を求めることができます。
例えば「2:3に内分する点を通る直線」など、共通テストにもよく出ます。
⸻
証明問題での応用
記述式で「この3点は一直線上にあることを示せ」など、
メネラウスの定理を逆に使って証明する問題もあります。丸暗記では対応できません。
⸻
「比」で考える図形の性質
図形における本質は「長さ」ではなく「比」であることが多いです。
チェバ・メネラウスはその代表例。「どこを基準に比をとるか」を意識しましょう。
定理の使い分けのポイント
覚え方はこれ!
• 点が三角形の内側 → チェバ
• 点が辺や延長線上 → メネラウス
図を描くことで、判断が劇的に早くなります。
⸻
チェバの定理の語呂合わせ
「チェバっと共点 1倍速」
比の積が「1」になる → 共点する
テンポよく覚えるのがコツです!
⸻
メネラウスの定理の語呂合わせ
「メネラに一直線の1本道」
「メネラ=一直線」+「比の積が1」
言葉と図をセットで覚えましょう。